题目描述:
There are some trees, where each tree is represented by (x,y) coordinate in a two-dimensional garden. Your job is to fence the entire garden using the minimum length of rope as it is expensive. The garden is well fenced only if all the trees are enclosed. Your task is to help find the coordinates of trees which are exactly located on the fence perimeter.
Example 1:
Input: [[1,1],[2,2],[2,0],[2,4],[3,3],[4,2]] Output: [[1,1],[2,0],[4,2],[3,3],[2,4]] Explanation: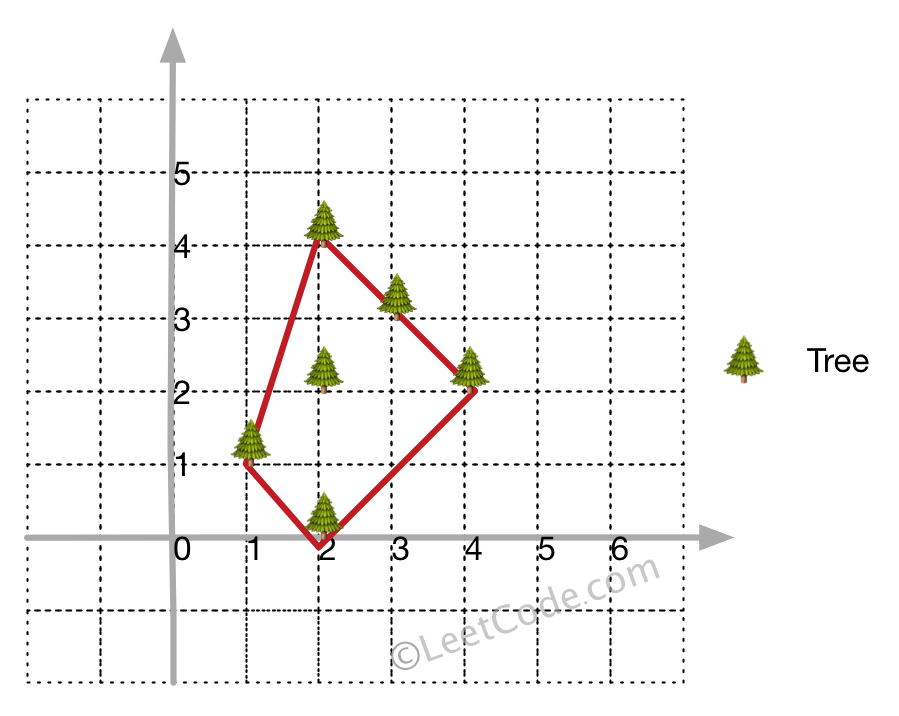
Example 2:
Input: [[1,2],[2,2],[4,2]] Output: [[1,2],[2,2],[4,2]] Explanation:Even you only have trees in a line, you need to use rope to enclose them.
Note:
- All trees should be enclosed together. You cannot cut the rope to enclose trees that will separate them in more than one group.
- All input integers will range from 0 to 100.
- The garden has at least one tree.
- All coordinates are distinct.
- Input points have NO order. No order required for output.
题目大意:
二维平面的花园里上有一些树,坐标(x, y)。用最短的绳子将这些树围起来。求围出图形边上的所有树的坐标。
注意:
- 所有树应该围在一起。不能围成多个组。
- 输入整数范围0到100。
- 花园至少有一棵树。
- 所有坐标不重复。
- 输入点坐标无序。输出也不需要有序。
解题思路:
凸包(Convex Hull)
解法I Graham扫描法
1. 求点集points中的最左下点lb
2. 以lb为原点,对points按照极坐标排序
3. 维护栈stack,初始将points[0], points[1]压入栈
4. 从2到len(points) - 1遍历各点i
重复弹出栈顶,直到points[-2], points[-1], points[i]非顺时针旋转未止
将points[i]压入栈
当最大极角对应的点超过一个时,这些点按照到lb的距离逆序排列。
Python代码:
# Definition for a point.
# class Point(object):
# def __init__(self, a=0, b=0):
# self.x = a
# self.y = b
class Solution(object):
def outerTrees(self, points):
"""
:type points: List[Point]
:rtype: List[Point]
"""
N = len(points)
if N <= 3: return points
lb = min(points, key = lambda p: (p.y, p.x))
ccw = lambda p1, p2, p3: (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x)
dsquare = lambda p1, p2: (p1.x - p2.x) ** 2 + (p1.y - p2.y) ** 2
cmp = lambda p, q: ccw(lb, q, p) or dsquare(p, lb) - dsquare(q, lb)
points.sort(cmp)
x = N - 1
while x and ccw(lb, points[x], points[x - 1]) == 0: x -= 1
points = points[:x] + points[x:][::-1]
stack = [points[0], points[1]]
for x in range(2, N):
while len(stack) > 1 and ccw(stack[-2], stack[-1], points[x]) < 0: stack.pop()
stack.append(points[x])
return stack
解法II Andrew's monotone chain 凸包算法
参阅:http://www.algorithmist.com/index.php/Monotone_Chain_Convex_Hull
伪代码:
首先根据x, y坐标对points从小到大排序
将U, L初始化为空(列表U, L分别存储凸包的上半部分和下半部分)
for i = 1, 2, ..., n:
while len(L) > 1 并且 L[-2], L[-1], points[i]非逆时针旋转:
L.pop()
L.append(points[i])
for i = n, n-1, ..., 1:
while len(U) > 1 并且 U[-2], U[-1], points[i]非逆时针旋转:
U.pop()
U.append(P[i])
将L和U的最后一个元素移除
L + U即为凸包(逆时针顺序)
Python代码:
# Definition for a point.
# class Point(object):
# def __init__(self, a=0, b=0):
# self.x = a
# self.y = b
class Solution(object):
def outerTrees(self, points):
"""
:type points: List[Point]
:rtype: List[Point]
"""
N = len(points)
if N <= 3: return points
lb = min(points, key = lambda p: (p.y, p.x))
ccw = lambda p1, p2, p3: (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x)
points.sort(key = lambda p: (p.x, p.y))
lo = []
for x in range(N):
while len(lo) > 1 and ccw(lo[-2], lo[-1], points[x]) < 0: lo.pop()
lo.append(points[x])
up = []
for x in range(N - 1, -1, -1):
while len(up) > 1 and ccw(up[-2], up[-1], points[x]) < 0: up.pop()
up.append(points[x])
return lo[:-1] + up[:-1]
本文链接:http://bookshadow.com/weblog/2017/05/15/leetcode-erect-the-fence/
请尊重作者的劳动成果,转载请注明出处!书影博客保留对文章的所有权利。
