题目描述：

LeetCode 576. Out of Boundary Paths

There is an m by n grid with a ball. Given the start coordinate (i,j) of the ball, you can move the ball to adjacent cell or cross the grid boundary in four directions (up, down, left, right). However, you can at most move N times. Find out the number of paths to move the ball out of grid boundary. The answer may be very large, return it after mod 10⁹ + 7.

Example 1:

Input:m = 2, n = 2, N = 2, i = 0, j = 0
Output: 6
Explanation: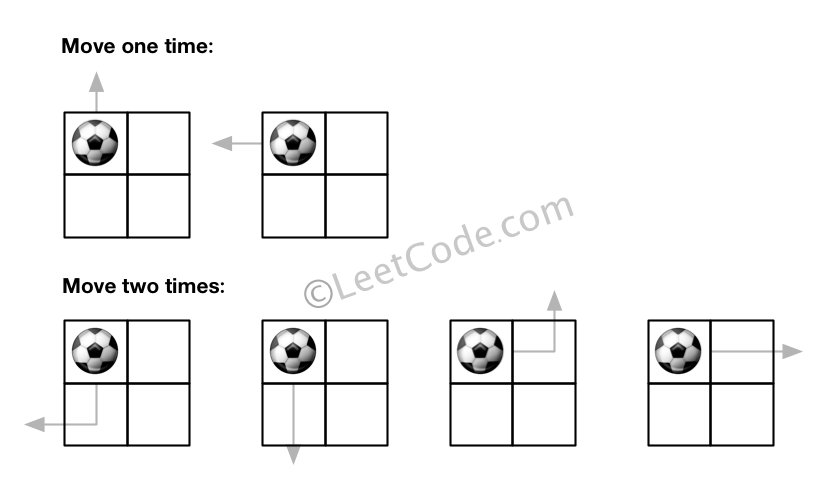

Example 2:

Input:m = 1, n = 3, N = 3, i = 0, j = 1
Output: 12
Explanation: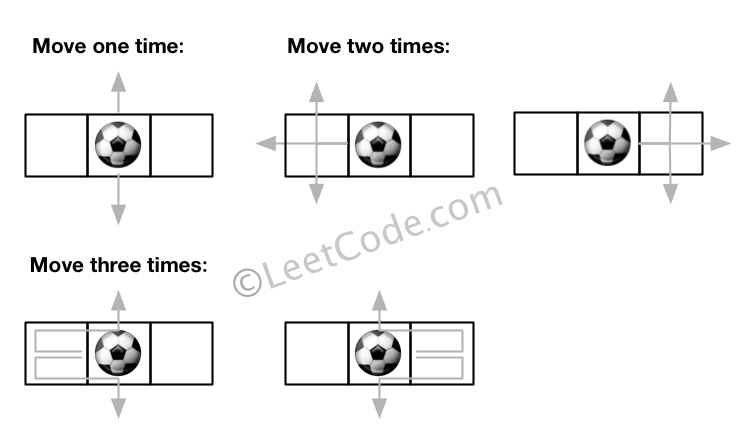

Note:

1. Once you move the ball out of boundary, you cannot move it back.
2. The length and height of the grid is in range [1,50].
3. N is in range [0,50].

题目大意：

给定m行n列格子和一个初始位置为(i, j)的球。球每次可以向上、下、左、右四个方向移动1个单位距离。

最多可以移动N次，求将球移出格子边界的所有路径数目。

由于结果可能会很大，将其对10^9 + 7取模。

注意：

1. 球一旦移出边界，就不能再移动回格子
2. 长度和宽度范围[1, 50]
3. N取值范围[0, 50]

解题思路：

动态规划（Dynamic Programming）

数组dp[t][x][y]表示第t次移动时，坐标x, y处的移动路径总数。

状态转移方程：

dp[t + 1][x + dx][y + dy] += dp[t][x][y]    其中t表示移动的次数，dx, dy 取值 (1,0), (-1,0), (0,1), (0,-1)

当x + dx或者y + dy超出边界时，将结果累加至最终答案。

Python代码：

class Solution(object):
    def findPaths(self, m, n, N, i, j):
        """
        :type m: int
        :type n: int
        :type N: int
        :type i: int
        :type j: int
        :rtype: int
        """
        MOD = 10**9 + 7
        dz = zip((1, 0, -1, 0), (0, 1, 0, -1))
        dp = [[0] *n for x in range(m)]
        dp[i][j] = 1
        ans = 0
        for t in range(N):
            ndp = [[0] *n for x in range(m)]
            for x in range(m):
                for y in range(n):
                    for dx, dy in dz:
                        nx, ny = x + dx, y + dy
                        if 0 <= nx < m and 0 <= ny < n:
                            ndp[nx][ny] = (ndp[nx][ny] + dp[x][y]) % MOD
                        else:
                            ans = (ans + dp[x][y]) % MOD
            dp = ndp
        return ans

 

本文链接：http://bookshadow.com/weblog/2017/05/07/leetcode-out-of-boundary-paths/
请尊重作者的劳动成果，转载请注明出处！书影博客保留对文章的所有权利。

如果您喜欢这篇博文，欢迎您捐赠书影博客： ，查看支付宝二维码