题目描述:
LeetCode 407. Trapping Rain Water II
Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.
Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Example:
Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] Return 4.
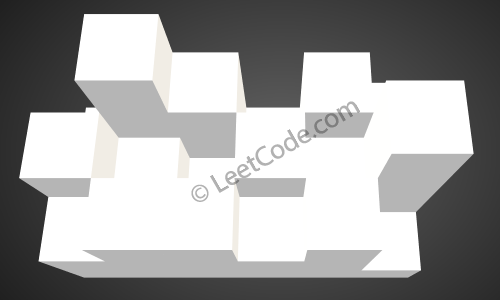
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.
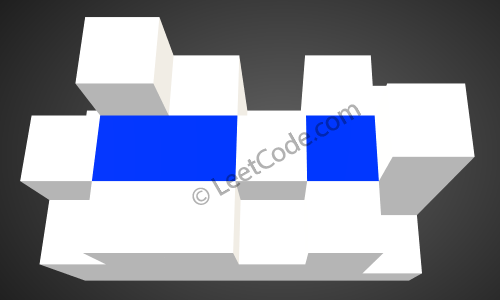
After the rain, water are trapped between the blocks. The total volume of water trapped is 4.
题目大意:
给定一个m x n正整数矩阵,表示一个二维高程图,计算降雨后其中可以蓄积的雨量。
注意:
m和n值均小于110.每一个单元的高度在(0, 20000)之间。
解题思路:
BFS(广度优先搜索)
记矩形的高度、宽度分别为m, n,令二维数组peakMap[i][j] = ∞,表示矩形区域最多可以达到的水面高度
将矩形的四条边中的各点坐标加入队列q,并将各点对应的高度赋值给peakMap相同坐标
每次从q中弹出队头元素x, y,探索其上、下、左、右四个方向nx, ny:
尝试用max(peakMap[x][y], heightMap[nx][ny]) 更新 peakMap[nx][ny] 的当前值(取两者中的较小值)
Python代码:
class Solution(object):
def trapRainWater(self, heightMap):
"""
:type heightMap: List[List[int]]
:rtype: int
"""
m = len(heightMap)
n = len(heightMap[0]) if m else 0
peakMap = [[0x7FFFFFFF] * n for _ in range(m)]
q = []
for x in range(m):
for y in range(n):
if x in (0, m - 1) or y in (0, n - 1):
peakMap[x][y] = heightMap[x][y]
q.append((x, y))
while q:
x, y = q.pop(0)
for dx, dy in zip((1, 0, -1, 0), (0, 1, 0, -1)):
nx, ny = x + dx, y + dy
if nx <= 0 or nx >= m - 1 or ny <= 0 or ny >= n - 1: continue
limit = max(peakMap[x][y], heightMap[nx][ny])
if peakMap[nx][ny] > limit:
peakMap[nx][ny] = limit
q.append((nx, ny))
return sum(peakMap[x][y] - heightMap[x][y] for x in range(m) for y in range(n))
另外一种解法:
蓄积雨水的单元格存在两种情况:
1. 单元格的高度严格小于其上、下、左、右方向的4个单元格高度 2. 单元格的高度小于或等于其上、下、左、右方向的4个单元格高度
对于情况1,可以利用“木桶原理”将其高度调整为四周单元格中的最小高度
对于情况2,可以通过DFS,寻找与其邻接的等高节点的四周高度的最小值
算法步骤如下:
首先,计算heightMap的和,记为sum0 然后,初始化队列queue,将所有邻接高度大于等于自己的点加入队列。 循环直到队列为空: 记队头为h 使用BFS寻找一个点集vs,其中的点与h等高,并且与h直接或者间接相邻。从而得到vs的最小临近点高度,记为minh。 将vs中的所有点从队列移除;如果minh > h,则将vs中所有点的高度更新为minh,并将h加入队尾; 再次计算heightMap的和,记为sum1,sum1 - sum0即为最终答案。
Java代码:
import java.awt.Point;
public class Solution {
private int m, n;
private int[][] heightMap;
private int dx[] = {1, 0, -1, 0};
private int dy[] = {0, 1, 0, -1};
public int trapRainWater(int[][] heightMap) {
this.heightMap = heightMap;
this.m = heightMap.length;
if (this.m > 0) this.n = heightMap[0].length;
int sum = calcHeightMapSum();
LinkedHashSet<Point> queue = new LinkedHashSet<Point>();
for (int i = 1; i < m - 1; i++) {
for (int j = 1; j < n - 1; j++) {
if (minNeighborHeight(i, j) >= heightMap[i][j]) {
queue.add(new Point(i, j));
}
}
}
while (!queue.isEmpty()) {
Point h = queue.iterator().next();
HashSet<Point> vs = new HashSet<Point>();
int minh = bfs(h, vs);
if (minh > heightMap[h.x][h.y]) {
for (Point e : vs) {
heightMap[e.x][e.y] = minh;
queue.remove(e);
}
queue.add(h);
} else {
for (Point e : vs) {
queue.remove(e);
}
}
}
return calcHeightMapSum() - sum;
}
private int bfs(Point p, HashSet<Point> vs) {
int ans = Integer.MAX_VALUE;
int height = heightMap[p.x][p.y];
LinkedList<Point> queue = new LinkedList<Point>();
vs.add(p);
queue.add(p);
while (!queue.isEmpty()) {
Point h = queue.removeFirst();
if (h.x == 0 || h.y == 0 || h.x == m - 1 || h.y == n - 1) {
ans = Math.min(heightMap[h.x][h.y], ans);
continue;
}
int minh = minNeighborHeight(h.x, h.y);
if (minh != height) {
ans = Math.min(minh, ans);
continue;
}
for (int k = 0; k < dx.length; k++) {
Point np = new Point(h.x + dx[k], h.y + dy[k]);
if (heightMap[np.x][np.y] != height) {
ans = Math.min(ans, heightMap[np.x][np.y]);
} else if (!vs.contains(np)) {
vs.add(np);
queue.add(np);
}
}
}
return ans;
}
private int minNeighborHeight(int i, int j) {
int minh = Integer.MAX_VALUE;
for (int k = 0; k < dx.length; k++) {
int di = i + dx[k];
int dj = j + dy[k];
minh = Math.min(minh, heightMap[di][dj]);
}
return minh;
}
public int calcHeightMapSum() {
int sum = 0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
sum += heightMap[i][j];
}
}
return sum;
}
}
本文链接:http://bookshadow.com/weblog/2016/09/25/leetcode-trapping-rain-water-ii/
请尊重作者的劳动成果,转载请注明出处!书影博客保留对文章的所有权利。
