题目描述：

LeetCode 802. Find Eventual Safe States

In a directed graph, we start at some node and every turn, walk along a directed edge of the graph.  If we reach a node that is terminal (that is, it has no outgoing directed edges), we stop.

Now, say our starting node is eventually safe if and only if we must eventually walk to a terminal node.  More specifically, there exists a natural number K so that for any choice of where to walk, we must have stopped at a terminal node in less than K steps.

Which nodes are eventually safe?  Return them as an array in sorted order.

The directed graph has N nodes with labels 0, 1, ..., N-1, where N is the length of graph.  The graph is given in the following form: graph[i] is a list of labels j such that (i, j) is a directed edge of the graph.

Example:
Input: graph = [[1,2],[2,3],[5],[0],[5],[],[]]
Output: [2,4,5,6]
Here is a diagram of the above graph.

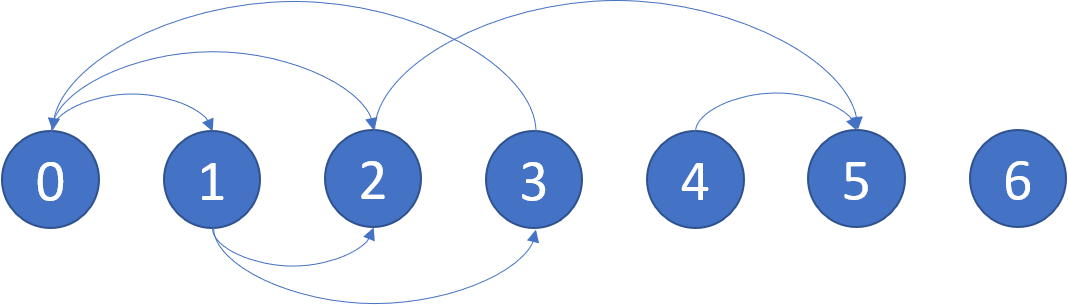
Note:

• graph will have length at most 10000.
• The number of edges in the graph will not exceed 32000.
• Each graph[i] will be a sorted list of different integers, chosen within the range [0, graph.length - 1].

题目大意：

给定有向图graph，求其中不存在环的节点列表。

解题思路：

拓扑排序（Topological Sort）

Python代码：

class Solution(object):
    def eventualSafeNodes(self, graph):
        """
        :type graph: List[List[int]]
        :rtype: List[int]
        """
        srcs = collections.defaultdict(set)
        tgts = collections.defaultdict(set)
        for idx in range(len(graph)):
            for v in graph[idx]:
                tgts[idx].add(v)
                srcs[v].add(idx)

        degZeros = [k for k in range(len(graph)) if not tgts[k]]
        while degZeros:
            ndegZeros = []
            for t in degZeros:
                for s in srcs[t]:
                    tgts[s].remove(t)
                    if not tgts[s]: ndegZeros.append(s)
            degZeros = ndegZeros
        return [k for k in range(len(graph)) if not tgts[k]]

 

本文链接：http://bookshadow.com/weblog/2018/03/18/leetcode-find-eventual-safe-states/
请尊重作者的劳动成果，转载请注明出处！书影博客保留对文章的所有权利。

如果您喜欢这篇博文，欢迎您捐赠书影博客： ，查看支付宝二维码