题目描述:
LeetCode 1168. Optimize Water Distribution in a Village
There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.
For each house i, we can either build a well inside it directly with cost wells[i], or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[i] = [house1, house2, cost] represents the cost to connect house1 and house2 together using a pipe. Connections are bidirectional.
Find the minimum total cost to supply water to all houses.
Example 1:
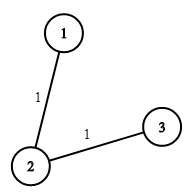
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]] Output: 3 Explanation: The image shows the costs of connecting houses using pipes. The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.
Constraints:
1 <= n <= 10000wells.length == n0 <= wells[i] <= 10^51 <= pipes.length <= 100001 <= pipes[i][0], pipes[i][1] <= n0 <= pipes[i][2] <= 10^5pipes[i][0] != pipes[i][1]
题目大意:
有n个村庄,给定数组wells和数组pipies。wells[i]表示在第i个村庄打井的花费,pipes的每个元素三元组(i, j, k) 表示村庄i到j铺设管道的花费为k。管道为双向连通。
求让每个村庄都有水的最小花费。
解题思路:
Kruskal(最小生成树)
Kruskal的基本思路是贪心(Greedy)。利用边集求最小生成树。首先对边集edges排序,然后遍历edges,利用并查集(Union-Find Set)对边的端点进行合并。若两端点不在同一个集合中,则将两端点进行merge,并记录权重。
本题在应用Kruskal之前需要稍作转换:构建虚拟节点n+1,将wells数组转化为每一个村庄1~n与n+1的边。
Python代码:
class Solution(object):
def minCostToSupplyWater(self, n, wells, pipes):
"""
:type n: int
:type wells: List[int]
:type pipes: List[List[int]]
:rtype: int
"""
for x, w in enumerate(wells):
pipes.append((x + 1, n + 1, w))
pipes.sort(key = lambda k: k[-1])
parents = {i:i for i in range(n+2)}
def find(i):
while i != parents[i]:
i = parents[i]
return i
ans = 0
for x, y, z in pipes:
x = find(x)
y = find(y)
if x != y:
ans += z
parents[x] = y
return ans
本文链接:http://bookshadow.com/weblog/2019/08/25/leetcode-optimize-water-distribution-in-a-village/
请尊重作者的劳动成果,转载请注明出处!书影博客保留对文章的所有权利。
